Parsing

This lecture discusses computational methods to perform syntactic parsing of sentences in free text.

What is Parsing and Why Parsing in Interesting

Parsing is the task of converting a sentence into a tree that captures syntactic relations among words. The key relations are:

Dependency: a word depends on another word if there exists a relation of agreement among them, or if transformations of movement or deletion of one word impose movement of deletion of the other.
Linear precedence: within a syntactic structure, words cannot appear in any order. Constraints on the linear order of words derive from the syntactic structure.

Parsing is important because it makes explicit the structure which is implicit within sentences. Explicit structure helps us perform tasks on sentences that would be difficult if performed on strings:

Sentence simplification
Sentence combination
Sentence transformation: negation, interrogation, change of tense, person.
Information extraction

We will review two distinct approaches to parsing:

Constituent-based parsing: the output is a tree of constituents; leaves are words; nodes above leaves are pre-terminal nodes (tagged by part of speech labels); interior nodes are constituents called phrases.
Dependency-based: all the nodes in the tree are words; links among words are labeled by syntactic function.

The following figure illustrates the different representations:

Representing Trees

We will first use the Scheme programming language to describe simple tree and context-free grammars concepts. Similar concepts are easily ported to Python - and we will review them next as we consider different parsing algorithms. The nltk tree module can be studied nltk.tree module documentation.

We encode trees as simple S-expressions (root . children). The following code captures this data structure:

;; Trees are of the form: (root . rhs) - where root is an interior node associated to a non-terminal
(define (new-tree cat rhs) (cons cat rhs))
(define (tree-root tree) (car tree))
(define (tree-children tree) (cdr tree))

Representing Grammars: Procedural Representation

A Context Free Grammar (CFG) is a simple mathematical model that can describe recursive syntactic structure. A CFG is defined by a 4-tuple (NT, T, S, R) where:

NT: is a set of non-terminal symbols (syntactic categories)
T: is a set of terminal symbols (words)
S - an element of NT - is the start symbol - the root of all legal trees described by the grammar
R is a set of rules. A rule has a structure (lhs --> rhs) where lhs is a non-terminal from NT and rhs is a (possibly empty) sequence of symbols from either NT or T.

The code in the following example is a Scheme translation of Common Lisp code from Peter Norvig, in the book Paradigms of Artificial Intelligence Programming. It is a procedural encoding -- that is, the non-terminal elements of the CFG are encoded by Scheme procedures. This procedural encoding allows us to generate strings covered by a non-terminal category. The key computational mechanisms to generate strings are:

Combining strings (we use the append scheme procedure)
Picking up one element out of a list of options (we use the one-of Scheme procedure)

String combination using append enforces the syntactic relation of linear precedence. The random choice of an option captures the fact that generating with a CFG is a non-deterministic operation. When we generate strings, non-determinism means picking an option randomly. When we parse (that is, try to find a legal tree covering an input string), non-determinism means searching for a legal option among multiple candidates.

;; Pick one element of set, and make a list of it.
(define (one-of set)
  (list (random-elt set)))

;; Choose an element from a list at random.
(define (random-elt choices)
  (list-ref choices (random (length choices))))

;; Return #t with probability 1/n
(define (flip n)
  (= (random n) 0))

;;; Version 1 of the grammar - no recursion
;;;
(define (sentence)    (append (noun-phrase) (verb-phrase)))
(define (noun-phrase) (append (Article) (Noun)))
(define (verb-phrase) (append (Verb) (noun-phrase)))
(define (Article)     (one-of '(the a)))
(define (Noun)        (one-of '(man ball woman table)))
(define (Verb)        (one-of '(hit took saw liked)))

This procedural encoding of CFGs can be used to generate trees that belong to the language defined by the grammar. Each time we run the procedure (sentence) we obtain a new random tree that belongs to the grammar.

The algorithm encoded by this procedural representation is a top-down expansion of the syntactic structure. Top-down traversals of recursive CFGs always has the potential to create infinite loops that must be explicitly avoided. If the grammar is recursive, an invocation of the generate can potentially go into an infinite loop. Look at the following example:

;;; Version 2: recursive grammar
;;; Note the problem of avoiding infinite recursion
;;; The parameter n=2 determines our preference for "deep" constituents.

(define (Adj*)
  (if (flip 2)
      '()
      (append (Adj) (Adj*))))

(define (PP*)
  (if (flip 2)
      (append (PP) (PP*))
      '()))

;; (define (noun-phrase) (append (Article) (Adj*) (Noun) (PP*)))
(define (PP) (append (Prep) (noun-phrase)))
(define (Adj) (one-of '(big little blue green adiabatic)))
(define (Prep) (one-of '(to in by with on)))

The category Adj* and PP* are recursive. If we define them naively, as shown below, the generation would always loop:

(define (Adj*) (append (Adj) (Adj*)))

If we want to explicitly encode the syntactic relation of dominance, we want to generate trees instead of strings. The following simple modification of the procedural encoding of CFGs generates trees:

;;; Version 2 of the grammar - generate trees instead of strings
;;;
(define (sentence)    (new-tree 'S (list (noun-phrase) (verb-phrase))))
(define (noun-phrase) (new-tree 'NP (list (Article) (Noun))))
(define (verb-phrase) (new-tree 'VP (list (Verb) (noun-phrase))))
(define (Article)     (new-tree 'DT (one-of '(the a))))
(define (Noun)        (new-tree 'N (one-of '(man ball woman table))))
(define (Verb)        (new-tree 'V (one-of '(hit took saw liked))))

Representing Grammars: Concrete Data Structure

The procedural encoding of CFGs shown above properly describes a specific algorithm to generate trees or strings from a CFG (in the example above, top-down depth-first development of the tree). If we want to use a different algorithm or perform a different task (for example, generate bottom-up or parse a string instead of generating, or generate from semantics instead of randomly, or generate with a different traversal order), we must use a different procedural encoding.

An alternative approach is to consider that the CFG is a concrete data structure (not procedural) that can be executed by various interpreters (one to generate, one to parse, etc). We develop this approach here by first describing a concrete data structure for CFGs.

;;; ==============================
;;; Explicit representation of grammars as list of rules
;;;
(define *simple-grammar*
  '((sentence -> (noun-phrase verb-phrase))
    (noun-phrase -> (article Noun))
    (verb-phrase -> (verb noun-phrase))
    (article -> the a)
    (noun -> man ball woman table)
    (verb -> hit took saw liked)))

;;; ==============================
;;; The Rule Abstract Data Type
;;;

;; The left hand side of a rule.
(define (rule-lhs rule)
  (car rule))

;; The right hand side of a rule.
(define (rule-rhs rule)
  (if (not (pair? rule))
    '()
    (cdr (cdr rule))))

;; Return a list of the possible rewrites for this non-terminal.
;; Each rewrite is the rhs of a rule whose lhs is the non-terminal.
;; Value is a list of lists of (non-terminal or terminal) nodes.
(define (rewrites grammar nt)
  (rule-rhs (assoc nt grammar)))

(define (non-terminal? grammar symbol)
  (not (null? (rewrites grammar symbol))))

;;; ==============================
;;; A grammar interpreter for top-down depth-first generation
;;;
;;  Append the results of calling fn on each element of list.
(define (mappend fn list)
  (apply append (map fn list)))

;; "Generate a random sentence or phrase"
;; Phrase can be:
;; - A single non-terminal to be expanded into a string S, NP...
;; - A list of non-terminals (NP VP)...
;; - A terminal
(define (generate grammar phrase)
  (cond ((list? phrase)
         (mappend (lambda (node) (generate grammar node)) phrase))
        ((non-terminal? phrase)
         (generate (random-elt (rewrites grammar phrase))))
        (else (list phrase))))

;;; ==============================
;;; We can run the same interpreter on a different grammar
;;;
(define *bigger-grammar*
  '((sentence -> (noun-phrase verb-phrase))
    (noun-phrase -> (Article Adj* Noun PP*) (Name) (Pronoun))
    (verb-phrase -> (Verb noun-phrase PP*))
    (PP* -> () (PP PP*))
    (Adj* -> () (Adj Adj*))
    (PP -> (Prep noun-phrase))
    (Prep -> to in by with on)
    (Adj -> big little blue green adiabatic)
    (Article -> the a)
    (Name -> Pat Kim Lee Terry Robin)
    (Noun -> man ball woman table)
    (Verb -> hit took saw liked)
    (Pronoun -> he she it these those that)))

;;; ==============================
;;; And can run a different interpreter on the same grammar
;;; This one generates a sentence with its parse-tree
;;;

;; Generate a random sentence or phrase, with a complete parse tree.
;; Return a single tree if phrase is a non-list value (non-terminal or terminal)
;; or a list of trees if phrase is a list of (non-terminal or terminal)
(define (generate-tree grammar phrase)
  (cond ((list? phrase)
         (map (lambda (node) (generate-tree grammar node)) phrase))
        ((non-terminal? phrase)
         (cons phrase
               (generate-tree grammar (random-elt (rewrites grammar phrase)))))
        (else (list phrase))))

;;; ==============================
;;; This interpreter generates all the sentences generated by a finite
;;; grammar (do not try it on *bigger-grammar* since it is recursive and infinite).
;;; This is a different approach to non-determinism: instead of 
;;; picking randomly one option, we compute all possible options
;;; in parallel.  The calls to random-elt and mappend are replaced
;;; by generate-all and combine-all.
;;; An alternative approach to non-determinism is to "search" for top-K expansions
;;; according to a scoring function, or to search for an expansion according to a
;;; acceptance-predicate (result is good), a search strategy and a heuristic.

;; Generate a list of all possible expansions of this phrase.
(define (generate-all grammar phrase)
  (cond ((null? phrase) (list '()))
        ((list? phrase)
         (combine-all (generate-all grammar (car phrase))
                      (generate-all grammar (cdr phrase))))
        ((non-terminal? phrase)
         (mappend (lambda (node) (generate-all grammar node)) (rewrites grammar phrase)))
        (else (list (list phrase)))))

;;  Return a list of lists formed by appending a y to an x.
;;  e.g., (combine-all '((a) (b)) '((1) (2)))
;;  -> ((A 1) (B 1) (A 2) (B 2))."
(define (combine-all xlist ylist)
  (mappend (lambda (y)
               (map (lambda (x) (append x y)) xlist))
           ylist))

This example shows three different interpreters for CFG generation applied on the same concrete data-structure. The Abstract-Data-Type for CFGs includes the methods: rule-lhs, rule-rhs, rewrites, non-terminal?. We now turn to the more complex problem of parsing a string using a CFG.

Parsing with CFGs

The parsing algorithm we show works bottom-up: we scan an input string left to right, and start to connect the words we meet to categories compatible with the CFG. The algorithm below computes all possible parses.

The state of the algorithm at a given step of the parsing is encoded by a data structure we call "parse". A partial parse describes a partial tree that covers a prefix of the string and the list of words not yet covered by the partial tree. The partial tree itself can be in two distinct modes: either it is completely connected to words in the sentence or some of its leaves are not yet instantiated -- that is, the partial tree is not "complete". 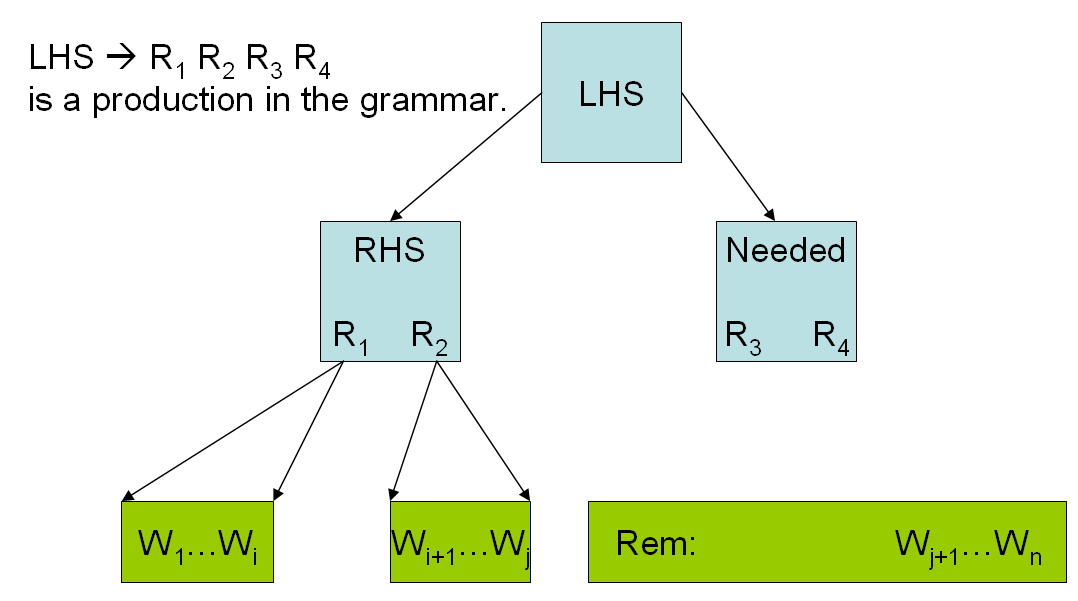The following diagram illustrates the general case of a partial parse.

;; ====================
;; Partial parse: a parse tree covering a prefix of a sentence and the remaining words of the sentence
;; ====================
(define (make-parse tree rem)
    (cons tree rem))
(define (parse-tree parse)
    (car parse))
(define (parse-rem parse)
    (cdr parse))

(define (parse-lhs parse) (tree-root (parse-tree parse)))

We call the two elements of the state of the parser parse-tree and parse-rem (for the remaining words). The root of the partial tree is accessed through the parse-lhs method.

When processing words, we match them to a pre-terminal symbol (a rule mapping a single terminal word to a non-terminal). The pre-terminals are either provided by the CFG in the form of rules of the form (NT --> word) or they are "guessed" by the parser for unknown words (that is, words that do not appear in the CFG). We could model this mapping by using a part-of-speech tagger as described in the previous chapter. In the code below, we use a simple strategy of allowing any unknown word to be covered by a rule of the form (OpenCategory --> word) for all open-class part-of-speech category.

;; ====================
;; Lexical rules
;; ====================

;; Categories to consider for unknown words
;; open-class parts-of-speech
(define *open-categories* '(N V A Name))
  
;; All rules that can produce word as rhs
;; This produces new (ambiguous) rules on the fly for "unknown" words
(define (lexical-rules grammar word)
    (let ((rules-in-grammar (find-all word grammar rule-rhs eq?)))
        (if (null? rules-in-grammar)
            (map (lambda (cat) (make-rule cat word)) *open-categories*)
            rules-in-grammar)))

When working bottom-up, the parser starts from a partial tree covering partially a prefix of the string to be parsed, and then tries to either expand the partial tree upwards or to the right. To expand the tree upwards, we must find a rule in the CFG that covers the root of the partial tree -- that is, a rule of the form (LHS --> cat RHS) where cat is the root of the current partial tree. We define the method rules-starting-with to search the CFG in this manner.

The termination criterion for the parser is that the partial-parse fully covers the sentence. We define the complete-parses function to filter the list of partial-parses maintained by the parser.

;; ====================
;; Search rules by prefix
;; ====================

;; Return a list of rules where cat starts the rhs.
(define (rules-starting-with grammar cat)
    (find-all cat grammar (lambda (rule) (first-or-nil (rule-rhs rule))) eqv?))

;; Those parses that are complete (have no remainder).
(define (complete-parses parses)
    (find-all-if null? parses parse-rem))

The core of the algorithm is implemented in 2 functions: the top-level function (parse words) returns a list of all possible partial-parses that cover any prefix of the list of words. The function that moves from one state of the parser to more advanced states is (extend-parse lhs rhs rem needed):

lhs: is the root of the partial tree that covers the prefix of the partial parse.
rhs: is the list of non-terminal or terminal nodes covered by the partial tree.
rem: is the list of words not yet covered by the partial tree.
needed: is the list of non-terminals on the end of the rhs of the partial tree that are needed to complete the partial-tree into a tree fully instantiated into lexical leaves.

The extend-parse function describes the two methods through which a partial tree can be expanded into a more advanced parse state:

Upwards: if the partial tree is "complete" (that is, all the non-terminals below the root expand down to lexical leaves), then return the partial tree and all its legal up-expansion (that is, trees of the form (UP partial-tree . needed)).
Rightwards: if the partial tree is not yet complete, then try to parse the remaining words (using a recursive call to parse on rem) and connect the partial-trees returned by this recursive call with the needed non-terminals on the bottom-right border of the partial tree.

;; ====================
;; Bottom-up parse algorithm
;; ====================

;;  Bottom-up parse, returning all parses of any prefix of words.
(define (parse words)
    (if (not (null? words))
        (mappend (lambda (rule)
                            (extend-parse 
                                (rule-lhs rule) 
                                (list (car words))
                                (cdr words) 
                                '()))
                    (lexical-rules (car words)))
        '()))

;; Look for the categories needed to complete the parse.
(define (extend-parse lhs rhs rem needed)
    (if (null? needed)
        ;; If nothing needed, return parse and upward extensions
        (let ((parse (make-parse (new-tree lhs rhs) rem)))
            (cons parse
                  (mappend
                        (lambda (rule)
                            (extend-parse (rule-lhs rule)
                                                (list (parse-tree parse))
                                                rem 
                                                (cdr (rule-rhs rule))))
                            (rules-starting-with lhs))))
      ;; otherwise try to extend rightward
      (mappend
            (lambda (p)
                (if (eq? (parse-lhs p) (car needed))
                    (extend-parse lhs 
                                        (append1 rhs (parse-tree p))
                                        (parse-rem p) 
                                        (cdr needed))
                    '()))
            (parse rem))))


;; ====================
;; Support
;; ====================

(define (append1 items item)
    (append items (list item)))

(define (first-or-nil x)
    (if (pair? x)
        (car x)
        '()))

;; List of items such that (pred (key item)) is #t
(define (find-all-if pred? items key)
    (cond ((null? items) '())
             ((pred? (key (car items))) (cons (car items) (find-all-if pred? (cdr items) key)))
             (else (find-all-if pred? (cdr items) key))))

;; List of i such that (pred? (key i) item) is #t
(define (find-all item sequence key pred?)
    (cond ((null? sequence) '())
             ((pred? item (key (car sequence))) (cons (car sequence) (find-all item (cdr sequence) key pred?)))
             (else (find-all item (cdr sequence) key pred?))))

This algorithm is not efficient because it keeps recomputing partial trees that do not lead to complete parses. This is caused mainly by the need for the recursive call to parse to match the needed right border of the current partial tree with a prefix of the remaining words. This recursive call is a "blind" attempt to build a tree that matches a known needed non-terminal. Hence, many of the partial trees returned by the recursive call will end up being thrown out by the test (if (eq? (parse-lhs p) (car needed)) ...).

There are two ways to improve on this situation:

Use memoization to remember the partial trees already computed.
Reduce the need for such blind search bottom-up + filter process.

We first show how to use simple general-purpose memoization on 3 functions: memoization of rules-starting-with and lexical-rules effectively indexes the concrete representation of the CFG by the keys used to search the rules. Memoization of the recursive parse function effectively turns the parser into a form of dynamic programming algorithm, that fills up a table of partial-trees covering substrings of the sentence to be parsed of increasing length.

;; ====================
;; Top level
;; ====================

;; Return all complete parses of a list of words.
(define (parser words)
    (clear-memoize 'parse)
    (map parse-tree (complete-parses (parse words))))

;; Switch to a new grammar.
(define (use grammar)
    (clear-memoize 'rules-starting-with)
    (clear-memoize 'lexical-rules)
    (set! *grammar* (map list->rule grammar))
    (length *grammar*))


;; ====================
;; Memoization support
;; ====================

;; If you use SISC (an excellent Java-based Scheme interpreter at http://sisc.sf.net)
;; load memoize.scm
;; This will replace these dummy definitions

;; Return a memo-function of fn.
;; test? must be eqv? eq? equal?
;; Memo is on (key args)
(define (memo fn test? key name) fn)
;; Clear the hash table from a memo function.
(define (clear-memoize fn-name) #t)

(set! lexical-rules (memo lexical-rules equal? car 'lexical-rules))
(set! rules-starting-with (memo rules-starting-with equal? car 'rules-starting-with))
(set! parse (memo parse eqv? car 'parse))

To demonstrate the effectiveness of the memoization process, try using the parser with the following "larger" grammars. The speed-up is considerable.

;; ====================
;;; Grammars
;; ====================

(define *grammar3*
  '((Sentence -> (NP VP))
    (NP -> (Art Noun))
    (VP -> (Verb NP))
    (Art -> the) (Art -> a)
    (Noun -> man) (Noun -> ball) (Noun -> woman) (Noun -> table)
    (Noun -> noun) (Noun -> verb)
    (Verb -> hit) (Verb -> took) (Verb -> saw) (Verb -> liked)))

(define *grammar4*
  '((S -> (NP VP))
    (NP -> (D N))
    (NP -> (D A+ N))
    (NP -> (NP PP))
    (NP -> (Pro))
    (NP -> (Name))
    (VP -> (V NP))
    (VP -> (V))
    (VP -> (VP PP))
    (PP -> (P NP))
    (A+ -> (A))
    (A+ -> (A A+))
    (Pro -> I) (Pro -> you) (Pro -> he) (Pro -> she)
    (Pro -> it) (Pro -> me) (Pro -> him) (Pro -> her)
    (Name -> John) (Name -> Mary)
    (A -> big) (A -> little) (A -> old) (A -> young)
    (A -> blue) (A -> green) (A -> orange) (A -> perspicuous)
    (D -> the) (D -> a) (D -> an)
    (N -> man) (N -> ball) (N -> woman) (N -> table) (N -> orange)
    (N -> saw) (N -> saws) (N -> noun) (N -> verb)
    (P -> with) (P -> for) (P -> at) (P -> on) (P -> by) (P -> of) (P -> in)
    (V -> hit) (V -> took) (V -> saw) (V -> liked) (V -> saws)))

Formal Definition of CFGs

To explain how the parsing algorithm can be made more efficient in practice, we now introduce the notion of CFG normal form. The formal definition of CFGs is:

G = {T,N,S,R}

T: set of terminals (lexicon)
N: set of non-terminals.  A subset P of N is called preterminals. Preterminals always rewrite as terminals.
S: start symbol (one of the nonterminals)
R: rules of the form X -> M where X is a nonterminal and is a sequence of terminals
and nonterminals (and may be empty).

We say that a grammar G generates a language L - the set of strings that can be accepted by a CFG recognizer (or equivalently that can be generated by the CFG generator).

Complexity of Parsing CFGs

CFGs can be parsed in O(n³) time, where n is the number of words in the sentence. The constant depends on the number of rules in the grammar. The following parsing algorithm called CYK demonstrates how this parsing complexity can be reached.

Chomsky Normal Form

The Chomsky Normal Form (CNF) for CFGs is defined as:

All rules are of the form either: 
    X --> Y Z (exactly two non-terminals in the RHS) 
 or X --> a (exactly one terminal) 
 or S --> epsilon (empty RHS - only S can rewrite as epsilon)

Any CFG can be converted into this form. The transformation algorithm from arbitrary CFG to CNF includes the following steps:

Conversion to CNF: Convert G into G' with L(G)=L(G')

1. Copy all conforming rules from G (binary or pre-terminal rules) to G' unchanged.

2. Remove Non-terminals that can generate epsilon (empty rules).

3. Convert terminals within rules to dummy non-terminals:
   For each terminal t, replace  rules (A --> L t R) by (A --> L N_t R) 
   (L and R are sequences of non-terminals).

4. Convert unit-rules:
   A unit-rule is a rule of the form (X --> Y), where Y is a non-terminal.
   Given (A -->* B) by only unit productions and (B --> R) is a nonunit rule,
   then add (A --> R)  to the new grammar and eliminate the unit rules.

5. Make all rules binary and add them to the new grammar:
   Replace (N --> X₁X₂X₃...X_n) with (N --> X₁R₁),  (R₁ --> X₂R₂), (R₂ --> X₃R₃) ...

NLTK contains code that transforms any tree to an equivalent binary tree, that could have been generated by a CFG in CNF in the treetransform module.

The CYK Parsing Algorithm

The CYK Algorithm is a dynamic programming algorithm that parses a CFG in CNF form in O(n³) time. The simplest form of CYK is a recognizer, which returns a boolean value indicating whether a string belongs to the language generated by a CFG:

Let the input be a string S consisting of  n characters: a₁ ... a_n.
Let the grammar contain r nonterminal symbols R₁ ... R_r. 
Let P[n,n,r] be an array of booleans. Initialize all elements of P to false.
For each i = 1 to n
  For each production R_j -> a_i, P[i,1,j] = true.
For each i = 2 to n -- Length of span
  For each j = 1 to n-i+1 -- Start of span
    For each k = 1 to i-1 -- Partition of span
      For each production RA -> RB RC
        P[j,i,A] = P[j,k,B] and P[j+k,i-k,C]

If any of P[1,n,x] is true (x is iterated over the set s, where s are all the indices for Rs)
  Then S is member of language
  Else S is not member of language

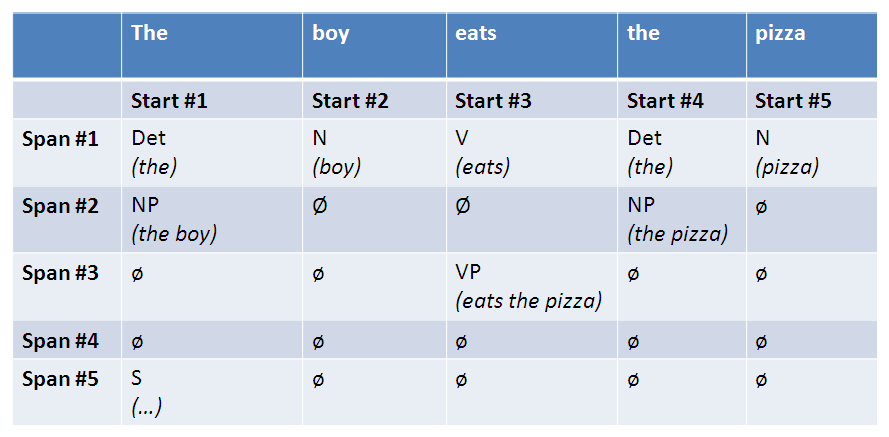
The Matrix P is filled incrementally bottom-up. The cell P[i, l, X] is True if the span of words starting at position i in S and of length l can be covered by a constituent of type X.

The following figure illustrates the state of the CYK matrix when parsing the sentence the boy eats the pizza:

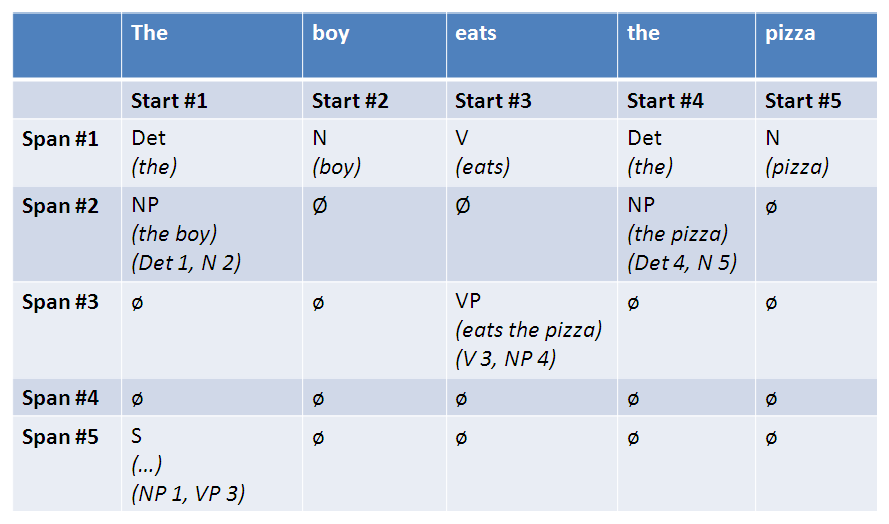
To obtain all the possible parse trees of a sentence S using CYK, one must extend the matrix P with back-pointers so that one can decode all legal trees one the matrix P has been filled. The backpointer indicates how to split a constituent P[j,i,A] at position j+k, and the label of the children B and C when a constituent (A --> B C) is constructed to cover the span (j, i+j). These backpointers are indicated in the following matrix:

Last modified June 7, 2012